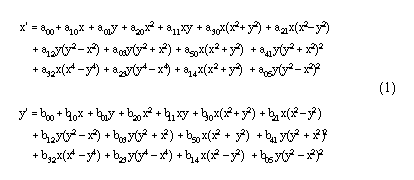Astrometric Precision and Accuracy
with HST FGS 3 in the Position Mode
A.L. Whipple, B. McArthur, Q. Wang, W.H. Jefferys,
G.F. Benedict, A.M. Lalich, P.D. Hemenway, E. Nelan,
P.J. Shelus, and D. Story
The University of Texas at Austin
Abstract
Three calibrations have been performed and analyzed by the Astrometry
Science Team since the first HST Calibration Workshop. These were a post-servicing
mission correction to the optical field angle distortion (OFAD), a cross
filter calibration, and a lateral color calibration. Descriptions of these
tests and the results of our analysis of the resulting data are given.
Key words: FGS, calibration, astrometry .
1. Introduction
The first servicing mission made no changes to the internal optics of the
three Fine Guidance Sensors (FGS) that are used for guiding and astrometry
on . However, the subsequent movement of the secondary mirror of the telescope
to the so-called "zero coma" position did change the morphology
of the FGS transfer functions because of the way the FGS interferometers
respond to the spherically aberrated beam from the telescope (Ftaclas et
al. 1993). This was anticipated and a post servicing mission calibration
plan was designed and executed. This paper reports the results of the three
post servicing calibration tests for which the Astrometry Science Team was
the primary analysis center.
2. Optical Field Angle Distortion Calibration
The Ritchey-Chrétien design of the optical telescope assembly of
HST, convolved with the optics of the FGS's, give rise to optical field
angle distortion (OFAD). The magnitude of these distortions is on the order
of 0.5 seconds of arc over the FGS field of view. Thus, the OFAD is the
most important source of systematic error in position mode astrometry done
with the FGS. The functional form of the OFAD has been known since before
launch. It can be described, to the level of one millisecond of arc, by
the two dimensional fifth order polynomial:
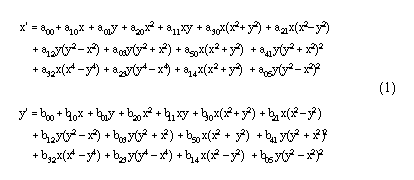
where x, y denote the observed position within the FGS field of view, x',
y' denote the corrected position, and the numerical values of the coefficients
a_ij and b_ij must be determined by calibration. Gravity release, outgassing
of the graphite-epoxy structures, and post-launch adjustment of the HST
secondary mirror required that the final determination of the OFAD coefficients
a_ij and b_ij be made by an on-orbit calibration.
Since there was no star field that was large enough and for which the relative
positions of the stars were known to the level of a millisecond of arc,
the positions of the stars had to be estimated simultaneously with the distortion
parameters. This was accomplished during a nineteen orbit calibration, executed
on 10 January 1993. Only FGS number 3 was calibrated in this way. The data
were analyzed to estimate the relative star positions, the pointing and
roll of the telescope during each orbit, the magnification of the telescope,
the OFAD polynomial coefficients, and several parameters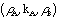 
that describe
the star selector optics inside the FGS. A complete description of that
calibration, the analysis of the data, and the results are given in Jefferys
et al. (1994).
Just prior to the 1993 OFAD calibration, a series of one orbit long-term
stability tests (LTSTAB) was initiated. An LTSTAB is run approximately once
per month and consists of a single pointing from the spring 1993 OFAD calibration
or its fall orientation counterpart. The LTSTAB is sensitive to scale and
low order distortion changes. The LTSTAB series immediately showed that
the scale measured by the FGS was changing with time. The most obvious indication
of this change was the large increase with time in the post-fit residuals
from a solution that solved for constant sets of star positions, star selector
parameters, and OFAD parameters (Fig.1a). The amount of scale change is
too large to be due to true magnification changes in the HST optical telescope
assembly. These changes may be due to water desorption in the graphite-epoxy
components within the FGS. This scale- like change is very well modeled
by a change in the star-selector-A effective lever arm. In response to our
early experience with these tests we modified our model to incorporate a
time dependent rA (Whipple et al. 1993). Figure 1b shows the effect Fig.
2. Differences (post-pre) between pre-servicing mission OFAD and the post-servicing
OFAD with rotation, scale, and shift removed. of including the time dependent
term in the analysis of the OFAD and LTSTAB data. The residuals from
the fit are decreased from as much as 50 mas in the x and 10 mas in y if
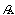is left constant (Fig. 1a) to about 10 mas in both coordinates
when 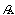is allowed to vary with time (Fig. 1b). Ten milliseconds
of arc is still about five times larger than our goal for the OFAD calibration.
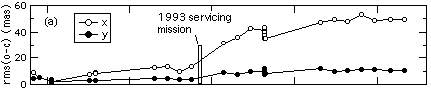
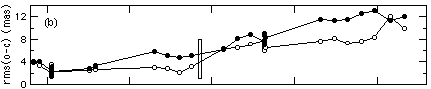
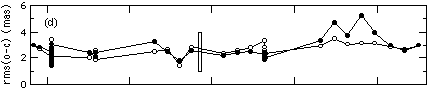
Fig. 1. Post-fit residuals from solutions that simultaneously fit the data
from the 1993 OFAD, 1994 -OFAD, and all LTSTAB calibration tests. Note the
significant improvement achieved by successive model modifications. (a)
5th order polynomial and star selector parameters held to values derived
from 1993 OFAD. (b) 5th order polynomial, rho_B, and k_A held fixed to 1993
OFAD values, separate values of rho_A estimated for each epoch of calibration
data. (c) 1992 through 1994 data reduced with 5th order polynomial, rho_B,
and k_A held fixed to 1993 OFAD values, 1994 to 1995 data reduced with 5th
order polynomial, rho_B, and k_A fit to 1994 -OFAD, separate values of rho_A
estimated for each epoch of calibration data. (d) 1992 through 1994 data
reduced with 5th order polynomial, rho_B, and k_A held fixed to 1993 OFAD
values, 1994 to 1995 data reduced with 5th order polynomial, rho_B, and
k_A fit to 1994 -OFAD, separate values of rho_A and 3rd order polynomial
coefficients estimated for each epoch of calibration data. (e) Same as (d)
but with the removal from the x component of all data of a four frequency
Fourier series that was fit to the 1993 OFAD data.
The HST servicing mission in December 1993 required that the secondary mirror
of the telescope be adjusted to optimize the performance of the refurbished
instruments. This caused a change in the FGS OFAD due in part to the effects
of the spherical aberration of the telescope, uncorrected at the FGS during
the servicing mission. This change can be seen clearly in Fig. 1b. A five
orbit -OFAD was performed on 27 April 1994 to restore the OFAD calibration
to the 1993 level. Significant changes in the OFAD, in addition to the scale-like
changes and at the level of 10 mas, were found (Fig. 2). Figure 1c shows
the improvement in the residuals from the fit to the OFAD and LTSTAB data
when two sets (one pre- servicing mission and one post-servicing mission)
of coefficients a_ij, b_ij in Eq. (1) are estimated. The root-mean-square
of the residuals is reduced to about 6 mas in both axes.
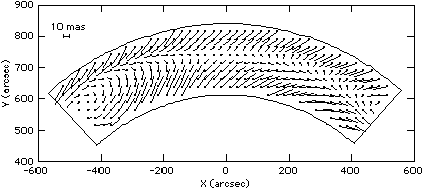
Fig. 2. Differences (post-pre) between pre-servicing mission OFAD and
the post servicing OFAD with rotation, scale, and shift removed.
The LTSTAB tests have revealed continued changes in the FGS. In addition
to the scale changes, we have begun to note higher order distortion changes.
These changes manifest themselves as something that looks like a radial
scale change and is fairly well modeled by changes in the third order terms
in Eq. (1). This is illustrated in Fig. 3 which compares two post-servicing
OFAD polynomials, one of which was fit to the 1994 five orbit 
calibration and the other of which had only the third order coefficients
adjusted to fit the 1995 day 170 LTSTAB data. Additionally, the LTSTAB data
taken in the fall orientation (which is rolled 180° from the spring
orientation) have never fit as well as the spring data. This has led us
to experiment with time dependent coefficients for the third order terms
in the Fig. 3. Differences 1994.117-LTSTAB 1995.170)
between the 3rd order distortions estimated from the post-servicing mission
-OFAD and those estimated from a spring 1995 LTSTAB orbit with rotation,
scale, and shift removed. OFAD polynomial. Estimating the third order coefficients
for each epoch of calibration data further reduces the residuals from the
fit to the OFAD and LTSTAB calibrations to about 3 mas in both axes although
the residuals for the data taken in the fall orientation are still higher
than the corresponding spring data (Fig. 1d).
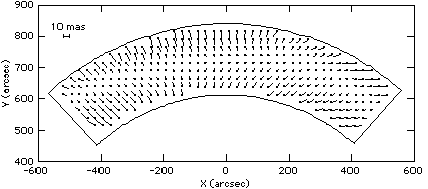
Fig. 3 Differences ( Delta-OFAD 1994.117-LTSAB 1995.170) between the
3rd order distortions estimated from the post-servicing mission Delta-OFAD
and those estimated from a Spring 1995 LTSTAB orbit with rotation, scale,
and shift removed.
We have also recently discovered a systematic signature in the residuals
from the analysis of the 1993 OFAD calibration. This appears as a very distinctive
curve in the x component residuals as a function of position angle in the
FGS field of view (Fig. 4). The curve cannot be modeled by the fifth order
polynomial. We have used a four frequency Fourier series to remove this
effect. The size of this effect, in an RMS sense over the entire field of
view of the FGS, is about one millisecond of arc. However, the peak-to-peak
values near the center of the field of view can be as large as 6 mas. The
addition of these terms to our model has reduced the residuals from the
OFAD and LTSTAB calibrations to about 2 mas in x (Fig. 1e). The residuals
in the y axis are unchanged at about 3 mas. The source of this unexpected
distortion is not known but it may be due to the way the FGS responds to
the spherically aberrated HST beam. This component of the distortion appears
to be very stable with time.
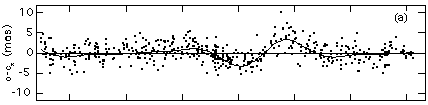
Fig. 4. Residuals from the 1993 OFAD calibration in the x axis (a) without
and (b) with a four frequency Fourier series removed.
On the basis of two and a half years of monitoring the distortions in FGS
3 we have concluded that at the level of a few milliseconds of arc, the
optical field angle distortion in HST FGS 3 changes with time. These changes
can be monitored and modeled by continuing the LTSTAB tests. There remains
some dichotomy between the OFAD calibration data taken in the spring and
that taken in the fall. A likely explanation for this is that the y components
of the distortions are not adequately sampled by the spring telescope pointings.
A new , in the fall orientation, is planned for November
1995. Fig. 4. Residuals from the 1993 OFAD calibration in the x axis (a)
without and (b) with a four frequency Fourier series removed.
3. FGS Astrometry Cross Filter Test and Calibration.
The astrometer Fine Guidance Sensor (FGS 3) has a filter wheel that contains
a broadband "clear" filter (F583W), a neutral density filter (F5ND),
a "yellow" filter (F550W), a somewhat narrower bandpass "clear"
filter centered on 6050 Å (F605W), and a pupil stop which reduces
the effective aperture to two thirds the full aperture (PUPIL). Any observation
of an object brighter than about 8th magnitude requires a filter other than
the F583W filter to be used. The F5ND filter, which reduces the intensity
by a factor of 100 (5 magnitudes) is the filter of choice, and is being
used to measure the separations of Hipparcos Stars with respect to extragalactic
objects. Because of manufacturing tolerances, a positional offset (wedge
effect) is expected between positions measured with different filters. On
day 200 of 1993, we obtained measurements of a Hipparcos star with respect
to an extragalactic object, where the Hipparcos star had a magnitude of
about 8.2. Because of a paucity reference stars, we were able to measure
the Hipparcos star as a primary target with the F583W filter and as a reference
star with the F5ND filter. A positional offset of about 4 mas with an error
of 2 mas was apparent in both coordinates. The measurement was not sufficient
to provide a definitive calibration, but was sufficient to prove, at the
two-sigma level, that a cross-filter calibration was required in order to
reduce the systematic error of the use of the F5ND filter to acceptable
levels. Therefore, a cross filter calibration test was proposed, accepted,
and executed. The results of that test are presented here. Fig. 5. The three
positions in the FGS 3 field of view in which the F583W/F5ND cross-filter
calibration was performed.
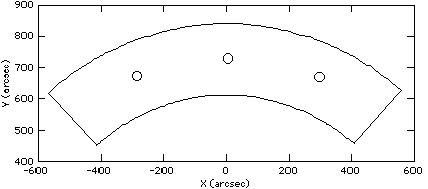
Fig. 5. The three positions in the FGS 3 field of view in which the
F583W/F5ND cross-filter calibration was performed.
The cross filter test provided us with three high quality data sets in three
positions in the FGS 3 field of view (Fig. 5). The data were analyzed in
several ways, all of which gave similar results. Eleven settings were made
using two filters on the same star, alternating between the F583W and the
F5ND filters, within one observation set. The analysis took the difference
between successive measurements through one filter and through the other
filter as a single data point, to correct for any uncompensated spacecraft
and/or FGS-to-FGS drift. Thus, 11 differences were obtained within each
observation set. The data had been pipelined and de-drifted prior to analysis.
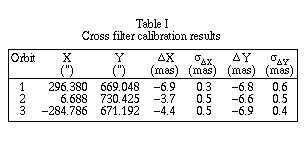
Table I gives the results. The sigmas are the standard deviations of the
means, and are probably smaller than realistic estimates of the external
errors. Still, the difference between the F5ND filter and the F583W filter
is significant in both x and y. In y, the measurements are consistent to
within 1 millisecond of arc. The difference in x appears to be field dependent.
We have settled on a piece-wise sub-field correction, dividing the FGS 3
field of view roughly in thirds and applying the x correction determined
from the calibration data for that third.
Thus far, the program that has used the F5ND filter the most has been the
measurement of the separation of Hipparcos Stars with respect to extragalactic
objects (EGO) to tie the Hipparcos reference frame to the VLBI reference
system. Currently, 19 observation sets with F5ND observations are being
used in the "link" solution. Two link solutions were performed:
one without the cross-filter corrections, and one with the cross-filter
corrections applied. In order to compare the two sets, we had to determine
whether each Hipparcos star-EGO pair was oriented with the Hipparcos star
at a larger (+) or smaller (-) value of the x coordinate than the EGO. The
mean residual with regard to that sign was then determined, with and without
the cross-filter correction applied. Without the cross-filter correction,
the mean residual for the (+) orientation was -6.1 mas. The (-) orientation
was +8.6 mas. With the cross-filter correction the mean residual for the
(+) orientation was -0.9 mas and for the (-) orientation was +2.3 mas. Note
that the data include all other error sources as well as the cross-filter
affect.
Therefore, we conclude that we have measured a significant cross filter
position shift in both x and y coordinates, and that applying that calibration
significantly improves the FGS measurements made when both F5ND and F583W
filters are used in the same observation set.
4. Lateral Color
Since each FGS contains refractive elements (Bradley et al. 1991), it is
possible that the position measured for a star could depend on its intrinsic
color. Changes in position would depend on star color, but the direction
of shift is expected to be constant, relative to the FGS axes. This lateral
color shift would be unimportant, as long as target and reference stars
have similar color. However, this is not always the case (e.g., Proxima
Centauri, Benedict et al. 1993), hence our interest. Pre-launch ground testing
indicated for FGS 3 a lateral color effect predominantly in the x direction,
with magnitude a few milliseconds of arc per unit change in B-V color index.
An on-orbit test was designed and conducted in December 1991. Due to excessive
spacecraft jitter (from a combination of the original solar arrays and insufficient
damping in the telescope pointing control system) and insufficient knowledge
of the OFAD, the results were inconclusive. A similar test was carried out
in December 1994. Preliminary analyses have failed to detect any measurable
lateral color signature. We continue detailed reanalyzes of these data,
motivated both by pre-launch predictions and by a fortuitous observation
of a very blue stellar flare on Proxima Centauri (a very red star). A position
shift observed during the flare indicates that lateral color may remain
an important source of systematic error.
5. Conclusions
We have shown that the methodology of the OFAD calibration of the Fine Guidance
Sensors can reduce this source of systematic error in positions measured
by the FGS's to the level of 2 mas. However, changes in the FGS units continue
to occur, even five years after launch. These changes require periodic updates
to the OFAD to maintain this critical calibration. The filter wedge effect
between the F583W and the F5ND filters has been successfully calibrated
in FGS 3. A lateral color effect in FGS 3 remains a possibility even though
two attempts to measure it have failed to detect this effect. Our analysis
of these data is continuing and additional on-orbit testing may be required
to settle this question.
References
- Bradley, A., Abramowicz-Reed, L., Story, D., Benedict, G., and W.
Jefferys: 1991, 'The Flight Hardware and Ground System for Hubble Space
Telescope Astrometry', PASP 103, 317
- Benedict, G.F., Nelan, E., McArthur, B., Story, D., van Altena, W.,
Ting-Gao, Y., Hemenway, P.D., Shelus, P.J., Whipple, A.L., Franz, O.G.,
Fredrick, L.W., and R.L. Duncombe: 1993, 'Periodic Low-Amplitude Variations
in the Brightness of Proxima Centauri', PASP 105, 487- 493
- Ftaclas, C., Nonnenmacher, A., Weindling, F., Story, D., and E. Nelan:
1993, 'Hubble Space Telescope Fine-Guidance-Sensor Transfer Function and
its Impact on Alignment and Guidance', Ap. Opt. 32, 1696
- Jefferys, W.J., Whipple, A., Wang, Q., McArthur, B., Benedict, G.F.,
Nelan, E., Story, D, and L. Abramowicz-Reed: 1994, 'Optical Field Angle
Distortion Calibration of FGS 3' in J.C. Blades and S.J. Osmer, ed(s).,
Calibrating Hubble Space Telescope, Space Telescope Science Institute,
Baltimore, 353-374.
- Whipple, A., Jefferys, W., Wang, Q., McArthur, B., Benedict, G.F.,
Nelan, E., Story, D., and L. Abramowicz-Reed: 1994, 'Maintaining the FGS
3 OFAD Calibration with the Long-Term Stability Test' in J.C. Blades and
S.J. Osmer, ed(s)., Calibrating Hubble Space Telescope, Space Telescope
Science Institute, Baltimore, 375-379